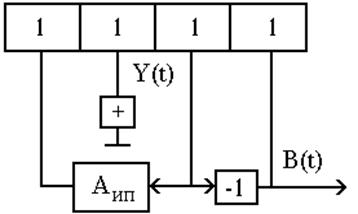
СОДЕРЖАНИЕ

ВОПРОСЫ ОБЕСПЕЧЕНИЯ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК ИЗМЕРИТЕЛЬНЫХ СИСТЕМ

Обеспечение требуемых точностных характеристик ИС при структурной коррекции может быть достигнуто в том случае, если КУ, за время накопления очередного кванта информации, получаемого от ИП, будет успевать обработать по заданному алгоритму предыдущий квант с заданной точностью. Естественно, что при больших скоростях изменения состояний УО, существенно возрастает объём информации, обработка которой требует увеличения скорости вычислительного процесса реализуемого КУ.

Если КУ не будет обеспечивать необходимую скорость вычислительного процесса, то это вызовет неизбежные потери информации и приведёт, соответственно к потере качества управления.

Чтобы избежать этого, на практике прибегают к построению КУ на базе цифровых специализированных вычислительных устройств [12], [62], [69], [100], [117]. Такие устройства получили широкое распространение и известны как цифровые КУ [3]. Их применение обусловлено прежде всего возможностью высокой скорости обработки информации, которая достигается за счёт распараллеливания вычислительного процесса и использования различных гибридных способов его организации [69], [85].

Вдобавок цифровые КУ также обладают существенно лучшими метрологическими характеристиками, по сравнению с КУ, реализуемыми на аналоговой элементной базе. Это объясняется отсутствием дрейфа нуля на выходе КУ, приводящего к возрастанию смещённой составляющей ошибки ИС, и что особенно важно, высокой устойчивостью к воздействию электромагнитных помех. Однако, применение цифровых КУ не исключает реализацию КУ на аналоговой элементной базе. Напротив, построение аналоговых КУ является важным этапом, на котором производится отладка методики расчёта их параметров, позволяющая добиться наиболее эффективной обработки сигналов от ИП, наиболее реально отражающих состояния УО.

Ещё одним важным аспектом, определяющим эффективность применения такой методики, является адекватность блока моделирования ИП в структурах КУ динамическим характеристикам применяемых датчиков. Понятно, что чем ближе блок моделирования ИП будет отражать динамические характеристики применяемого датчика, тем точнее будет выполняться условие (1.14), и соответственно, тем лучше будут точностные характеристики ИС [8].

В качестве простейшей модели ИП, обладающего инерционностью можно использовать апериодическое звено c ПФ:

W(p)=1/(Т_n+1), (1.10)

которое характеризуется двумя параметрами: статическим коэффициентом передачи - k и постоянной времени - Т_n. Параметры k и T можно определить по переходной характеристике звена, полученной при подаче на его вход единичного ступенчатого воздействия в качестве тестового сигнала.

Величина параметра k равна уровню асимптоты (t->), величина параметра T равна времени, за которое переходная характеристика достигает 1-exp(-1)»0.63 уровня этой асимптоты. В некоторых случаях возникает необходимость усложнения модели ИП до системы двух и более апериодических звеньев, соединенных последовательно. Такое включение имеет место всегда, если применяемые ИП состоят из нескольких блоков, осуществляющих многократные превращения энергии [50], [60], [82].

Рассмотрим ряд существующих структур КУ и отметим их достоинства и недостатки с точки зрения обеспечения ими эффективного подавления помех в сигналах от ИП.

Структура КУ, представленная на Рис.1.5, реализует оператор А_ип^-1, методами, описанными в [20].

Рис.1.5. Структура КУ с прямым обращением оператора.

Однако при этом, она характеризуется низкой помехоустойчивостью, в силу того, что получаемый оператор А_ип^-1 обладает дифференцирующими свойствами. Реализация оператора А_ип^-1 может быть выполнена с помощью структуры КУ на обратимых сумматорах [81] (Рис.1.6). Однако при этом, такая структура также обладает дифференцирующими свойствами, что приводит к снижению её помехоустойчивости.

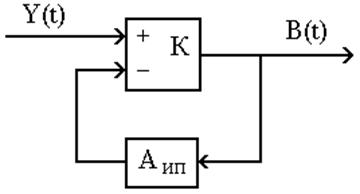
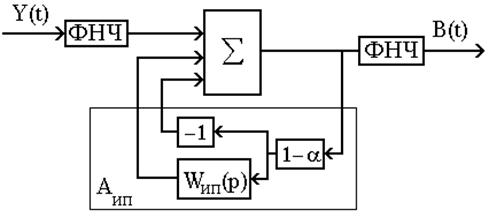
Результатом ещё одного известного подхода, описанного в [81], является структура КУ, представленная на Рис.1.7, где блок, реализующий оператор А_ип, включается в обратную связь операционного усилителя (сумматора) с бесконечно большим коэффициентом усиления k->.

Рис.1.6. Структура КУ на обратимых сумматорах.

Рис.1.7. Структура КУ с включением блока А_ип в цепь обратной связи сумматора

Такое устройство обладает низкой помехоустойчивостью. С целью обеспечения устойчивости такой структуры КУ к воздействию помех, коэффициент усиления операционного усилителя k делают большим, но конечным. Применение идеи регуляризации [86] предполагает коэффициент k=1/a, что позволяет несколько повысить помехоустойчивость такой структуры КУ. Однако, при этом существенным её недостатком является наличие смещённой составляющей ошибки в выходном сигнале операционного усилителя, которая зависит от параметра регуляризации α.

Большой интерес, представляет метод декомпозиционной регуляризации, предложенный в [60] для построения КУ. Одним из основных результатов этого метода является принцип многокаскадности, применительно к структурной организации КУ, что позволило добиться ККИ ИП в несколько десятков раз, по сравнению с рассмотренными структурами КУ при идентичных уровнях воздействующих помех. Такой принцип является наиболее приемлемым в тех случаях, когда ИП состоит из нескольких последовательно соединенных блоков. Каждый из каскадов КУ рассматривается, как автономное КУ, реализующее обратный оператор по отношению к каждому промежуточному блоку ИП. Вследствии этого, помехоустойчивость каждого каскада значительно выше по сравнению с однокаскадным вариантом КУ. Остановимся более подробно на рассмотрении нескольких структур КУ, построенных с использованием этого метода.

Рис 1.8. Структура КУ с использованием ФНЧ.

На Рис.1.8 представлена структура КУ, реализующая ПФ:

W_ку=1/(W_ип(p)+α), (1.11)

При этом, устойчивая работа имеет место лишь для α≠0, что естественным образом исключает возможность достижения идеальной компенсации инерционности ИП. Практически, достичь этого можно настолько близко, насколько это позволяет уровень помех в измерительном сигнале от ИП. Поэтому, обеспечение необходимой помехоустойчивости КУ, в этом случае достигается за счёт дополнительной низкочастотной фильтрации выходных сигналов ИП и КУ реализованного в [1], [2], [60], посредством их пропускания через сглаживающие фильтры низких частот (ФНЧ).

Другая структура КУ представлена на Рис.1.9. Она реализует ПФ:

W_ку=1/(W_ип(p)+α-αW_ип(p)), (1.12)

Её отличие от предыдущей структуры КУ заключается в несколько другом способе введения блока, реализующего разность (1-α). Это позволило достигнуть независимости постоянной (смещённой) составляющей выходного сигнала КУ от параметра регуляризации α=1/k, что соответственно привело к практическому отсутствию смещённой составляющей ошибки на выходе КУ. Помехоустойчивость этой структуры КУ, как и в предыдущем случае, обеспечивается аналогичным способом, реализованным в [60].

Рис.1.9. Структура КУ с использованием ФНЧ, со стабилизацией постоянной составляющей на выходе.

Таким образом, рассмотренные структуры КУ позволяют обрабатывать сигналы, отражающие реальные состояния УО по искаженным измерительным сигналам, получаемым от ИП. Однако при этом, все они обладают существенным недостатком - низкой помехоустойчивостью. Это накладывает существенное ограничение на их применение в ИС, эксплуатируемых в условиях с повышенными уровнями помех. В двух последних рассмотренных структурах КУ, эту проблему частично удалось решить посредством введения параметра регуляризации α->0 и низкочастотной фильтрации входных и выходных сигналов КУ с помощью сглаживающих ФНЧ. Такой подход обладает существенными недостатками.

Как известно, сигналы при прохождении через частотные фильтры претерпевают неизбежные нелинейные искажения [32], которые так или иначе приводят к увеличению смещённой составляющей ошибки ИС. Кроме этого, частотные фильтры подразделяются на два обширных класса: пассивных и активных фильтров.

Пассивные фильтры, обладают как правило коэффициентом передачи k≤1, что требует дополнительного повышения коэффициента усиления КУ с целью обеспечения требуемого уровня его выходного сигнала необходимого для дальнейшей обработки в БУ. В свою очередь, повышение коэффициента усиления становиться неприемлемым из-за приближения КУ к порогу устойчивости.

Активные фильтры обладают коэффициентом передачи k≥1, обеспечиваемым применением в их структурах полупроводниковых элементов (операционных усилителей, транзисторов и т.д.), обладающих, как правило, низкой температурной стабильностью характеристик. В частности, это проявляется в наличии температурного дрейфа нуля на выходе фильтров [32] и КУ, обуславливающего возникновение смещённой составляющей ошибки. Понятно, что это становится также неприемлемым. Не менее важным аспектом, ограничивающим применение частотных фильтров в трактах измерения являются их стоимостные характеристики. Они тем выше, чем выше эффективность применяемых частотных фильтров. На практике, это приводит к резкому усложнению структур частотных фильтров, и, как следствие, к непомерному увеличению аппаратных затрат на их разработку и практическую реализацию.

Отметим несколько существенных недостатков метода декомпозиционной регуляризации. Увеличение числа каскадов КУ при обработке сигналов от ИП, состоящих из нескольких блоков, неизбежно приводит к накоплению смещённой составляющей ошибки ИС. В частности это проявляется в возрастании динамической погрешности ИС (типа задержки). Это особенно хорошо заметно в цифровых КУ, где появление нового каскада приводит в лучшем случае к необходимости использования дополнительного такта при реализации рекурсивной части устройства. Попытки реализации устойчивой обработки искажённых сигналов от ИП, состоящих из нескольких блоков, однокаскадной структурой КУ (Рис.1.9), не привели к положительным результатам [60], из-за низкой устойчивости получаемого переходного процесса при ККИ≥1,5.

В результате отмеченных достоинств и недостатков рассмотренных структур КУ можно сделать вывод о том, что каскадирование КУ и применение частотной фильтрации их входных и выходных сигналов позволяет повысить помехоустойчивость ИС, но при этом неизбежно приводит к снижению их точностных характеристик, и, как следствие, к потере качества контроля и управления объектами в технологических процессах, при резком увеличении аппаратных затрат. Такое положение вещей приводит к необходимости разработки специализированных аналоговых и эквивалентных им цифровых КУ, позволяющих эффективно компенсировать инерционность ИП и осуществлять подавление помех в сигналах от ИП при минимальных аппаратных затратах.