СОДЕРЖАНИЕ

СТРУКТУРА И ПРИНЦИПЫ ФУНКЦИОНИРОВАНИЯ СПЕЦИАЛИЗИРОВАННОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

Разработка КУ, позволяющих эффективно компенсировать инерционность ИП и подавлять действие помех, представляет достаточно сложную и актуальную проблему, решаемую способами, рассмотренными в предыдущей главе.

Как было указано, их реализация на практике приводит к непомерно высоким аппаратным затратам, что в существующих технико-экономических условиях становится не приемлемым.

Одним из методов, позволяющим разрабатывать специализированные КУ для эффективной компенсации инерционности ИП и подавления действующих помех при минимуме аппаратных и стоимостных затрат, является метод динамической коррекции [18], [22], [33], [34], [39], [40], [52], [87], [88], [89], [91], [92], [93], [94], [96], [110]. Его применение основано на введении в структуру КУ звена динамической коррекции.

Важным достоинством этого метода является также и то, что он ориентирован на реализацию средствами аналоговой и гибридной вычислительной техники. Это как нельзя лучше подходит для его применения на основе, уже имеющихся в наличии вычислительных средств [68].

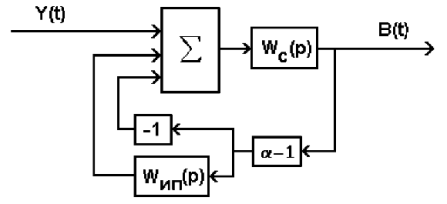
В соответствии с методом динамической коррекции представлена разработанная структура специализированного КУ (Рис.2.1), позволяющая эффективно осуществлять компенсацию инерционности ИП и подавление действующих помех, а также методика расчёта его параметров [96].

Рис.2.1. Структура специализированного КУ.

Структура специализированного КУ реализует ПФ:

, (2.8)

где α - параметр регуляризации;

W_ип(р) - ПФ ИП, моделируемого апериодическим звеном:

, (2.9)

где T_k - коэффициенты, которые определяются экспериментально и характеризуют инерционность ИП;

W_с(р) - ПФ звена динамической коррекции, реализующего в общем виде дробно-рациональную ПФ:

. (2.10)

Y(t), B(t) - соответственно входной и выходной сигналы специализированного КУ.

Для эффективной компенсации инерционности ИП и подавления действующих помех, необходимо выбором ПФ звена динамической коррекции W_с(р) достигнуть повышения порядка ПФ ИС на n единиц таким образом, чтобы порядок его ПФ был больше, либо равным порядку ПФ ИП (n ≥ k). Величину n необходимо в каждом конкретном случае выбирать с учётом компромисса между повышением эффективности компенсации инерционности ИП и подавления действующих помех с одной стороны, и возрастанием затрат на реализацию специализированного КУ с другой.

Подставим (2.9) и (2.10) в (2.8) и выполним необходимые преобразования. В результате получим:

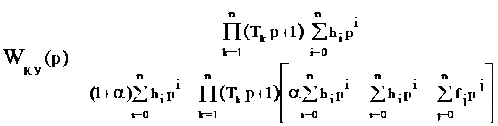. (2.11)

Для обеспечения апериодичного характера переходного процесса на выходе специализированного КУ, необходимо чтобы все коэффициенты характеристического уравнения

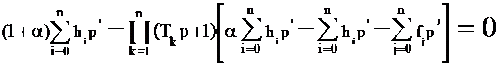, (2.12)

были положительными, а его корни были вещественными и отрицательными. Отметим, что коэффициенты T_n в (2.9) отличны от нуля и задаются априори. Полагая коэффициент h₀≠0, при любом количестве коэффициентов h_i=0 или их сокращении, всегда можно подобрать коэффициенты f_j звена динамической коррекции W_с(р) таким образом, чтобы все коэффициенты при степенях p_j характеристического уравнения (2.12) были положительны. Тогда ПФ звена динамической коррекции W_с(р) можно записать в виде:

, (2.13)

где выбор коэффициентов f_j сводится к разработке методики расчёта соотношений, по которым можно найти их численные значения. В последующих разделах этой главы будет рассмотрена методика расчёта соотношений для следующих случаев:

1) Подавление специализированным КУ действующих помех (без применения низкочастотной фильтрации) и компенсация инерционности ИП, моделируемых апериодическим звеном первого порядка.

2) Компенсация специализированным КУ инерционности ИП, моделируемых апериодическим звеном второго порядка.

3) Подавление специализированным КУ действующих помех (без применения низкочастотной фильтрации) наряду с компенсацией инерционности ИП, моделируемых апериодическим звеном второго порядка.

Заметим, что все три случая рассмотрены для структуры специализированного КУ в аналоговом варианте.

Теперь, определим точностные характеристики ИС (Рис.2.2).

Рис.2.2. Представление ИП в виде фильтра.

Найдём результирующую погрешность ИП при воздействии помех. Тогда согласно [106] её можно представить в виде двух составляющих. Первая составляющая соответствует регистрируемой величине, отражающей состояния УО, прошедшей через ИП с ПФ статической и динамической погрешностей. Вторая - помехе, прошедшей через ИП с этой же ПФ. Представим ИП виде фильтра с ПФ - F(jω), приведённого на Рис.2.2. На вход ИП поступает величина Y(t), отражающая регистрируемое состояние УО. На ИП действует заранее неизвестный случайный сигнал n(t), рассматриваемый как помеха. Измеряемый сигнал на его выходе обозначим через σ(t).

Если ИП обладает свойствами линейности [11], [114], то его характеристики полностью определяются ПФ - F(jω). Найдём мгновенную погрешность воспроизведения σ_м(t) измерительного сигнала на выходе ИП:

σ_м(t) =[S(t) - Y(t)], (2.14)

где Y(t) реальное значение измерительного сигнала. В силу того, что ИП обладает инерционностью, между сигналами σ(t) и Y(t) имеет место временной сдвиг, определяемый временем переходного процесса t_п.п., выражение (2.14) можно записать в виде:

σ_м(t) =[S(t-t_п.п.) - Y(t)], (2.15)

Вычислим интенсивность помех в измерительном сигнале от ИП, которую, согласно [15], можно представить в виде:

, (2.16)

где σ_σм(ω) - спектральная плотность мгновенной погрешности воспроизведения σ_м(t). Если спектральная плотность регистрируемой величины Y(t) на входе ИП известна, то спектральная плотность измерительного сигнала на его выходе определяется согласно [13] выражением:

, (2.17)

где S_y(ω) - спектральная плотность регистрируемой величины Y(t). При отсутствии помех, ИП должен преобразовывать регистрируемую величину Y(t) в измерительный сигнал без искажений. Это значит, что идеальная ПФ ИП равна единице, т.е. F(jω)=1. Вследствие наличия потерь энергии в процессе съёма и преобразования, инерционности ИП, его реальная ПФ отличается от единицы, и разность 1-F(jω) можно рассматривать, как ПФ суммы статической и динамической погрешности ИП - σ_ст+σ_д=σ₁. Тогда, спектральная плотность на выходе ИП определяется соотношением:

. (2.18)

Запишем выражение для суммы статической и динамической погрешности воспроизведения ИП при реализации регистрируемой величины Y(t), отражающей произвольное состояние УО:

. (2.19)

Выражение (2.19) в дальнейшем будем называть смещённой составляющей ошибки ИП. Так как на входе ИП наряду с регистрируемой величиной Y(t), отражающей произвольное состояние УО, действует помеха n(t) со спектральной плотностью σ_n(ω), то его результирующая погрешность возрастает на величину несмещённой оставляющей ошибки ИП:

, (2.20)

тогда, в соответствии с правилами сложения, результирующая погрешность ИП определяется выражением:

. (2.21)

Отметим, что выражение (2.21) в дальнейшем будем называть величиной ошибки, вносимой ИП, и как следствие ИС.

На основании конкретного вида W_с(р) определим точностные характеристики ИС, содержащей разработанное специализированное КУ, а также определим критерии выбора параметра регуляризации α.

Рис. 2.3. Структура ИС, содержащей специализированное КУ.

Аналогично (2.21) запишем выражение для величины ошибки ИС, содержащей разработанное специализированное КУ:

σ²_ис = σ²_см + σ²_нс, (2.22)

где σ_см - смещённая составляющая ошибки, появляющаяся вследствии отличия ПФ специализированного КУ от точной обратной ПФ ИП; σ_нс - несмещённая составляющая ошибки, возникающая вследствии наличия помех n(t) в измеряемом сигнале на выходе ИП.

Определим зависимость смещённой составляющей ошибки σ_см от параметра регуляризации α для ИС (Рис.2.3), содержащей специализированное КУ при подаче на вход ИП единичного ступенчатого воздействия вида:

Y(t) = a, a = 1(t) (2.23)

Перейдём с использованием преобразований Лапласа в область изображений Y(p) ÷ Y(t). Тогда в области изображений для (2.23) можно записать:

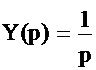. (2.24)

Запишем согласно [88] выражение для смещённой составляющей ошибки ИС:

, (2.25)

где W_ис(p) - результирующая ПФ ИС, содержащей специализированное КУ и определяемая как:

. (2.26)

Выполним необходимые подстановки в (2.26) и получим:

. (2.27)

Подставим (2.24) и (2.27) в (2.25) и выполним дальнейшие преобразования с учётом того, что при t-> параметр р следует положить равным нулю. В результате получим искомое соотношение, определяющее зависимость смещённой составляющей ошибки σ_см от параметра регуляризации α для ИС, содержащей специализированное КУ:

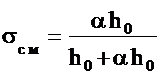, (2.28)

Анализируя соотношение (2.28) можно сделать вывод от том, что смещённая составляющая ошибки σсм возрастает при увеличении параметра регуляризации α.

Определим зависимость несмещённой составляющей ошибки σ_нс от параметра регуляризации α для ИС (Рис.2.3), содержащей специализированное КУ при подаче на его вход случайного сигнала (помехи), который представляет собой белый шум n(t) с нормальным законом распределения и дисперсией D_σ:

, (2.29)

где σ_n(ω) - спектральная плотность белого шума n(t). Спектральная плотность сигнала σ_ку(ω) на выходе специализированного КУ определяется соотношением:

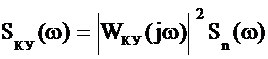, (2.30)

Дисперсия Δ_вых сигнала на выходе специализированного КУ определяется соотношением:

. (2.31)

Преобразуем (2.31) к виду:

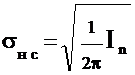, (2.32)

где

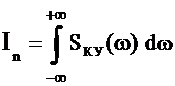. (2.33)

Интеграл I_n в общем случае при любом n для устойчивой системы может быть представлен в виде:

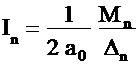, (2.34)

где Δ_n совпадает с точностью до знака со старшим определителем матрицы Гурвица

, (2.35)

, (2.36)

где b_i и a_i - коэффициенты соответственно полиномов числителя и знаменателя ПФ (2.11), R - степень полинома знаменателя ПФ (2.11). Рассмотрим зависимость от параметра регуляризации α знаменателя I_n и числителя M_n соответственно.

Заметим, что знаменатель I_n имеет вид 2a₀Δ_n. Исходя из соответствующих свойств определителей запишем, что если αi, входящие в любой, произвольным образом выбранный столбец (строку) Δ_n пропорциональны α, то Δ_n следовательно, пропорционален α, если же таких столбцов (строк) два, то Δ_n пропорционален α² и т.д. Анализируя знаменатель ПФ (2.11) специализированного КУ нетрудно заметить, что он содержит коэффициенты, пропорционально зависящие от параметра регуляризации α. Вследствие этого знаменатель I_n также пропорционален α.

Руководствуясь описанными свойствами определителей, для числителя M_n следует отметить, что он не зависит от α, так как коэффициенты числителя ПФ (2.11) не зависят от параметра регуляризации α.

Таким образом, исходя из свойств знаменателя I_n и числителя M_n можно сделать вывод о том, что несмещённая ошибка σ_нс уменьшается при увеличении параметра регуляризации α.

Отметим, что в общем случае величина ошибки σ_ис в случае, когда σ_см≠0 и σ_нс≠0, имеет минимум, который достигается для параметра регуляризации α, удовлетворяющего условию:

Δσ_ис/Δα = 0. (2.37)

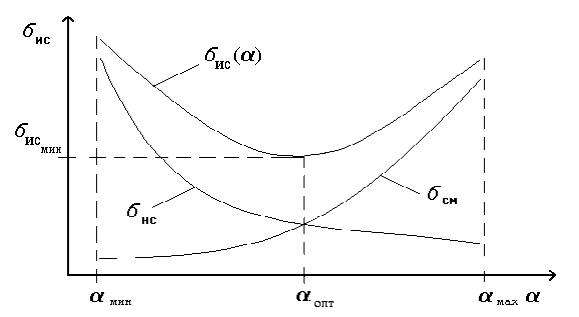
Зависимость величины ошибки σ_ис от параметра регуляризации α можно интерпретировать посредством графической зависимости [42], приведённой на Рис.2.4:

Рис.2.4. Зависимость величины ошибки ИС от величины параметра регуляризации α.

Откуда видно, что существует такое значение параметра регуляризации α, при котором величина ошибки σ_ис(α) становится минимально возможной.

Таким образом, зная величину ошибки σ_ис, можно пользуясь соотношением (2.37) определить наиболее приемлемую величину параметра регуляризации α, с точки зрения обеспечения наиболее эффективной компенсации специализированным КУ инерционности ИП и подавления действующих помех. Следует указать, что параметр регуляризации α, может быть выбран также в соответствии с любыми другими известными критериями. Например по критерию невязки [64], критерию квазиоптимальности и отношения [58], или по способу модельных (эталонных примеров) [19], [21].

В качестве практической рекомендации по обеспечению эффективного процесса компенсации специализированным КУ инерционности ИП и подавления действующих помех важно отметить, что эта задача решается последовательно в два этапа. На первом этапе, выбирая корни p_n характеристического уравнения ПФ (2.8) специализированного КУ, устанавливают требуемый ККИ ИП. На втором этапе выбирая величину параметра регуляризации α, добиваются минимального уровня искажений в выходном сигнале специализированного КУ.