Лабораторная работа № 1ИССЛЕДОВАНИЕ ПРОХОЖДЕНИЯ СИГНАЛОВ ЧЕРЕЗ RC-ЦЕПИ1. Цель работыИсследование частотных и импульсных характеристик простейших RC-цепей, экспериментальное определение граничных частот и импульсных параметров таких цепей и связи между ними. 2. Схемы эксперимента и методика исследованияИсследование схем осуществляется методом математического моделирования с помощью программы Orcad 9.2 [2]. В ее среде "собираются" и "исследуются" RC-цепи с интегрирующим (Рис. 1) и разделительным (Рис.2) конденсатором, снимаются их частотные и переходные характеристики, определяются основные параметры этих цепей.
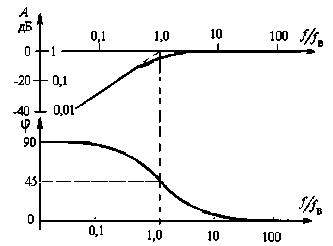
3. Основные сведенияRC-цепи в электронике применяются часто [1]. Изображенная на Рис. 1 схема представляет собой простейший RC-фильтр нижних частот, который без изменений передает низкочастотные и обеспечивает затухание высокочастотных сигналов и их запаздывание по фазе относительно входных сигналов. Частотная характеристика НЧ-фильтра (Рис. 1) может быть представлена в комплексной форме следующим образом: A(jω) = 1/(1+jωRC) Отсюда получаем выражение для амплитудно-частотной характеристики: Выражение для фазочастотной характеристики будет иметь такой вид: φ(ω) = - arctg(ωRC) или φ(f) = - arctg(f/fB) Здесь fв = 1/2πRC - верхняя граничная частота НЧ-фильтра. Рис. 3. АЧХ и ФЧХ НЧ-фильтра На частоте среза коэффициент передачи A(fв) = 1/√2 = 0,707, что в логарифмическом масштабе соответствует - З дБ. Фазовый сдвиг на этой частоте равен -45°. Графики АЧХ и ФЧХ изображены на Рис. 3, где видно амплитудно-частотную характеристику наиболее просто составить из двух асимптот: • на нижних частотах (f<fв) A(f) = 1 => 0 дБ; • на высоких частотах (f>fB) A(f) ≈ fв/f, т.е. коэффициент усиления обратно пропорционален частоте. Таким образом, при увеличении частоты в 10 раз коэффициент усиления уменьшается тоже в 10 раз. А это эквивалентно наклону -20 дБ на декаду для характеристики, построенной в логарифмическом масштабе. На рис.2 изображен другой простейший RC-фильтр верхних частот. Он без изменений передает высокочастотные сигналы и обеспечивает затухание низкочастотных. Его частотная характеристика в комплексной форме может быть представлена следующим образом: Отсюда получаем выражение для амплитудно-частотной характеристики: Выражение для фазочастотной характеристики будет иметь такой вид: φ(ω) = - arctg(1/ωRC) или φ(f) = - arctg(fH/f) Здесь fн = 1/2πRC - нижняя граничная частота или частота среза ВЧ-фильтра. На частоте среза коэффициент передачи A(fв) = 1/√2 = 0,707, что в логарифмическом масштабе соответствует - З дБ. Фазовый сдвиг на этой частоте равен +45°. Рис. 4. АЧХ и ФЧХ ВЧ-фильтра Графики АЧХ и ФЧХ для ВЧ-фильтра изображены на Рис. 4. Как и для НЧ-фильтра амплитудно-частотную характеристику в двойном логарифмическом масштабе наиболее просто составить из двух асимптот: • на высоких частотах (f > fн) A(f) = 1 => 0 дБ; • на низких частотах (f « fн) A(f) ≈ f/fн, т.е. коэффициент усиления пропорционален частоте. Таким образом, при увеличении частоты в 10 раз коэффициент усиления тоже увеличивается в 10 раз. А это эквивалентно наклону + 20 дБ на декаду для характеристики, построенной в двойном логарифмическом масштабе. Для анализа схем (Рис. 1 и 2) во временной области на вход надо подать прямоугольный импульс напряжения. Выражение для переходной характеристики в этом случае можно записать в виде Uвых(t) = Uвых(∞) - [Uвых(∞) - Uвых(0)] e-t/τ, где
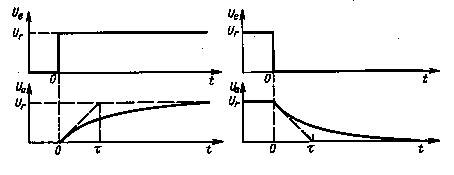
Диаграммы выходного напряжения для схемы НЧ-фильтра (Рис. 1) при разных скачках входного сигнала показаны на Рис.5, а для схемы ВЧ - фильтра (Рис. 2) на Рис. 7 и 8. а) б) Рис. 5. Переходные процессы в НЧ-фильтре На частоте среза коэффициент передачи A(fв) = 1/√2 = 0,707, что в логарифмическом масштабе соответствует - З дБ. Фазовый сдвиг на этой частоте равен +45°. Для интегрирующей цепи (Рис. 2) характерно наличие фронта (Рис. 5,а) или среза (Рис. 5,б) в выходном сигнале. Время нарастания (среза) импульса можно определить из общей формулы где Uвых (t1) и Uвых (t2) ~ выходное напряжение в соответствующие моменты времени и Uвых ( Тогда время фронта, определяемое по уровням 0,1 ... 0,9, равно tф = 2,2τ. Для среза аналогично tc = 2,2τ. Для интегрирующей цепи (Рис.2) возможны два случая: 1. Постоянная времени для этой схемы мала по сравнению с длительностью входного сигнала (tвх » τ). Конденсатор в этом случае называется дифференцирующим или укорачивающим. За время действия входного импульса он успеет полностью зарядиться или разрядиться. Таким образом, перепад входного напряжения приведет к появлению на выходе конечного по длительности импульса положительной (Рис. 6, а) или отрицательной (Рис. 6, б) полярности. Длительность этого импульса, определенного по уровню 0,5, можно рассчитать по формуле tu вых ~ 0,7τ. а) б) Рис.
6.
Переходные процессы в ВЧ-фильтре при большой длительности входного сигнала (tн>> 2. Длительность входного сигнала мала по сравнению с постоянной времени (tвх << τ). В этом случае напряжение на конденсаторе за время действия входного сигнала не успеет существенно измениться, и форма выходного сигнала практически повторит форму входного импульса. Конденсатор в этом случае называется разделительным или конденсатором связи. Однако на выходе будет спад плоской вершины выходного импульса Δu (Рис. 7). Рис. 7. Переходные процессы в ВЧ-фильтре при малой длительности входного сигнала (tн<<t) Относительный спад плоской вершины Δu рассчитывается по формуле: Δu = (tвх/τ)•100%; Данной формулой можно пользоваться, если Δu не превосходит 10 ... 15%. 4. Подготовка к работеДля схемы с интегрирующим (Рис. 1) и разделительным (Рис. 2) конденсатором: • получить выражение для амплитудно-частотной UBыx(f) и переходной UBыx(t) характеристик; • построить данные зависимости и по графикам определить:
• рассчитать выше указанные параметры и сравнить с графическим расчетом, а результаты занести в таблице 2. Параметры элементов схемы и длительность входного сигнала приведены в таблице 1. Номер варианта соответствует порядковому номеру студента в учебном журнале. Таблица 1. Варианты заданий
5. Рабочее заданиеВ CАПР Orcad 9.2 используя программу «Schematics» выполнить отрисовку принципиальной схемы для исследования частотных и импульсных свойств RC-цепи с интегрирующим и разделительным конденсатором (Рис. 8): Рис. 8. Рабочая схема для исследования RC-цепей в частотной и временной области. Показаны маркеры для вывода напряжения в Вольтах при временном анализе и для вывода напряжения в децибелах при частотном анализе • Открыть библиотеку элементов (Draw - Get New Part) и используя ее разместить на рабочем поле все требуемые элементы схемы. Искать нужные элементы удобно по их именам: источник входного напряжения - VPULSE, резистор - R, конденсатор - С, земля - АGND. • Расположить элементы на рабочем поле в соответствии с принципиальной схемой Рис. 8, не соединяя их. Для этого на элемент, с которым надо что-то сделать, поместить курсор мыши и щелкнуть его левой кнопкой. При этом элемент окрасится. Отмеченный элемент можно повернуть (Ctrl/R), удалить (Delete) или переместить. В последнем случае отмеченный элемент захватить мышью и, нажав на левую кнопку, переместить в нужное место, после чего кнопку отпустить. • Соединить элементы на рабочем поле в соответствии с принципиальной схемой. Для этого курсор мыши перевести в режим рисования соединительных линий (иконка - карандаш с тонкой линией). Подвести карандаш к выводу одного из элементов и щелкнуть левой кнопкой (ЛК). Подвести карандаш к другой точке схемы и снова щелкнуть ЛК. И так далее. Для отмены режима рисования щелкнуть правой кнопкой. • Ввести обозначения элементов в соответствии с Рис. 8. Для этого дважды щелкнуть на элемент, а лучше на его имя. В всплывающем окне откорректировать имя. • Установить параметры резисторов и конденсаторов. Для этого дважды щелкнуть на элемент, а лучше на его параметр. В всплывающем окне установить значение параметра. Параметры компонентов схемы приведены в табл. 1. • Установить параметры источника напряжения V. Для этого дважды щелкнуть на элемент. В всплывающем окне установить указанные параметры. Для частотного анализа:AC = 1v - амплитуда входного сигнала равна 1В на всем частотном диапазоне. Для временного анализа:V1 = 0 - минимальное значение импульсного сигнала равно нулю; V2 = 1v - максимальное значение импульсного сигнала равно 1В; TD = 0 - задержка импульса относительно начала временного анализа равна нулю; TR = 0 - передний фронт импульса равен нулю; TF = 0 - задний фронт импульса равен нулю; PW = ... us - длительность импульса (tu, в мкс) для каждого варианта задана в табл. 1. • Сохранить схему в рабочей папке, например, D:\Student\<name>, где <name> - любое имя не включающее кириллицу и пробелы, или какое-либо другое по указанию преподавателя. Примечание: Имя папки и файла схемы не должно содержать русских букв и не должно находиться на Рабочем столе операционной системы. 2. Снять амплитудно-частотные характеристики RC-цепей. Для этого необходимо: • Установить режим анализа по переменному току (Analysis/Setup - AC Sweep): Decade - изменение частоты по логарифмическому закону; Pts/Decade = 101 число точек на декаду; Start Freq = 10 - начальная частота; End Freq = 1Meg - конечная расчетная частота. • Подключить к обоим выходам схемы (см. Рис. 8) специальный маркер измерения коэффициента передачи в децибелах (Markers - Mark Advanced - Vdb). В этом случае выходной сигнал (а так как Uвх = 1В, то и коэффициент усиления) измеряется в децибелах: Кdb= 20 Lg(Uвых/Uвх). • Запустить расчет схемы (F11 или пиктограмма
• Воспользовавшись электронным курсором (пиктограмма
3. Снять временные характеристики RC-цепей. Для этого необходимо: • Отключить анализ частотных характеристик и установить режим анализа во временной области (Analysis/Setup - Transient): - Print Step = 20 ns - шаг вывода данных; - Final Time = ...us - конечное время расчета (в мкс) зависит от варианта и определяется примерно как 2tн; • К входу и выходам схем вместо маркера Vdb подключить маркер для измерения напряжения (Markers - Voltage или пиктограмма
• Запустить расчет схемы (F11 или пиктограмма
• Воспользовавшись двумя электронными курсорами определить для схемы Рис. 1 по уровням 0,1...0,9 фронт выходного напряжения tф. Для схемы Рис. 2 с помощью курсоров определить амплитуду выходного импульса А и спад плоской вершины А. По этим данным рассчитать относительный спад плоской вершины Δu. 8. Результат записать в табл. 2 и сравнить с с полученными расчетными данными. Таблица 2. Результаты проведенных исследований
4. Исследовать дифференцирующую RC-цепь (Рис.2). Для этого необходимо: • Уменьшить емкость конденсатора С2 в 50 ... 100 раз. • Установить маркеры для вывода напряжения только на входе и выходе исследуемой схемы. • Запустить расчет схемы (F11 или пиктограмма
• С помощью электронных курсоров по уровню 0,5 определить длительности положительного и отрицательного импульсов. • Сравнить полученный результат с расчетным временем.
Литература1. Электротехника и электроника. Учебник для вузов. - В 3-х кн. Кн. 3. Электрические измерения и основы электроники/ Г.П. Гаев, В.Г. Герасимов, О.М. Князьков и др.; Под ред. проф. В.Г. Герасимова. - М.: Энергоатомиздат, 1998. 2. В.Д. Разевиг. Система проектирования OrCAd 9.2. - М.: Издательство СОЛОН, 2001. - 519с. 3. Афанасьев А. О., Кузнецова С. А., Нестеренко А. В. Проектирование в OrCAD. Киев. «Наука и техника», 2001. 4. Ленк Дж. Электронные схемы: Практическое руководство. пер с англ. - М. Мир, 1985. - 343 с. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все права на информацию для посетителей разрешены © 2011 - 2024 - Zadereyko.INFO





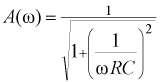
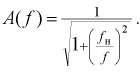




 ) и получить амплитудно-частотные характеристики
RC - цепей.
) и получить амплитудно-частотные характеристики
RC - цепей.
 ).
).