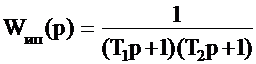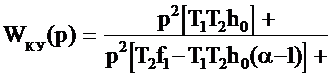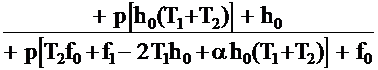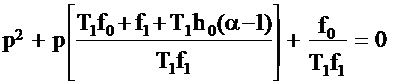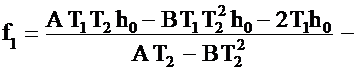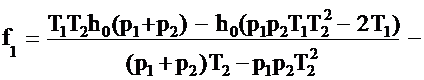СОДЕРЖАНИЕ

ВЫБОР ПАРАМЕТРОВ ЗВЕНА ДИНАМИЧЕСКОЙ КОРРЕКЦИИ, ОБЕСПЕЧИВАЮЩИЙ КОМПЕНСАЦИЮ ИНЕРЦИОННОСТИ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ, МОДЕЛИРУЕМЫХ АПЕРИОДИЧЕСКИМ ЗВЕНОМ ВТОРОГО ПОРЯДКА

Рассмотрим предлагаемую методику расчёта соотношений для нахождения численных значений коэффициентов звена динамической коррекции W_c(p) для случая моделирования ИП апериодическим звеном второго порядка [92], [93] с ПФ:

. (2.49)

С целью обеспечения компенсации инерционности ИП и максимальной простоты специализированного КУ, выберем порядок ПФ звена динамической коррекции W_c(p) равным единице, т.е. с ПФ (2.39).

Подставим (2.39), (2.49) в (2.8) и стремясь к наиболее простому виду W_c(p), на основании [95] положим h₁=T₁h₀. Тогда ПФ специализированного КУ будет описываться соотношением:

. (2.50)

Запишем характеристическое уравнение ПФ (2.50) в виде:

. (2.51)

Положим в (2.51) коэффициенты при p равными соответственно:

. (2.52)

Система двух уравнений (2.52) содержит три неизвестных h₀, f₀, f₁. Зададимся коэффициентом h₀=const. Тогда численные значения коэффициентов f₀ и f₁ могут быть найдены по соотношениям:

, (2.53)

. (2.54)

Подставим (2.45), (2.46) в (2.53) и (2.54), и запишем соотношения, по которым можно найти численные значения коэффициентов f₀ и f₁:

, (2.55)

. (2.56)

Из полученных соотношений (2.55) и (2.56) видно, что численные значения коэффициентов f₀ и f₁ задаются корнями p₁ и p₂ характеристического уравнения (2.51), коэффициентами T₁ и T₂ ПФ (2.49) и параметром регуляризации α. Численное значение коэффициента h₀ выбирается исходя из его максимальной простоты реализации в специализированном КУ.

Следует отметить, что разработанная методика выбора параметров звена динамической коррекции W_c(p) позволяет исключить декомпозицию специализированного КУ на каскады при компенсации инерционности ИП моделируемых апериодическим звеном второго порядка.