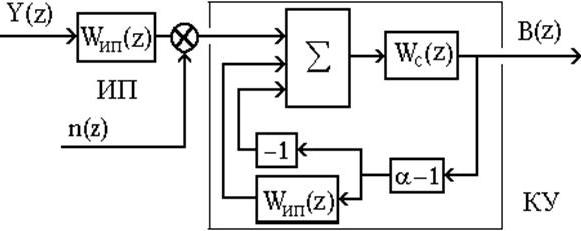
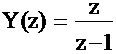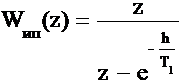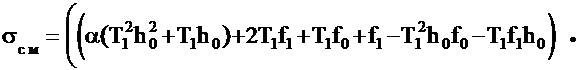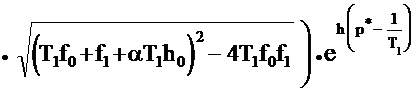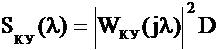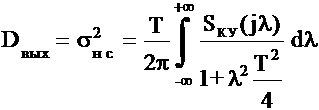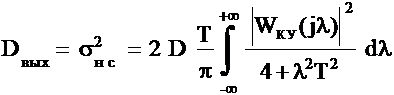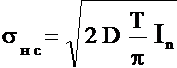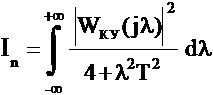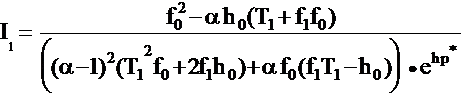СОДЕРЖАНИЕ

ОЦЕНКА ТОЧНОСТНЫХ ХАРАКТЕРИСТИК ИЗМЕРИТЕЛЬНОЙ СИСТЕМЫ, СОДЕРЖАЩЕЙ ЦИФРОВОЕ СПЕЦИАЛИЗИРОВАННОЕ КОРРЕКТИРУЮЩЕЕ УСТРОЙСТВО

Определим величину ошибки ИС (Рис.3.1), содержащей цифровое специализированное КУ. Заметим, что величина ошибки sис включает в себя смещённую и несмещённую составляющие, и определяется соотношением (2.7).

Рис.3.1. Структура ИС, содержащей цифровое специализированное КУ.

Найдём соотношение, определяющее зависимость смещённой составляющей ошибки σ_см от параметра регуляризации α для ИС (Рис.3.1), содержащей цифровое специализированное КУ при подаче на вход ИП единичного ступенчатого воздействия вида:

. (3.29)

Запишем выражение для смещённой составляющей ошибки ИС:

, (3.30)

где W_ис(z) - результирующая ПФ ИС, содержащей цифровое специализированное КУ и определяемая как:

. (3.31)

Отметим, что дискретная ПФ ИП, моделируемого апериодическим звеном первого порядка имеет вид:

, (3.32)

а W_ку(z) описывается дискретной ПФ (3.8).

Выполним необходимые подстановки в (3.29) и дальнейшие преобразования с учётом того, что при h->∞ параметр z следует положить равным единице.

В результате получим искомое соотношение, определяющие зависимость смещённой составляющей ошибки σ_см от параметра регуляризации α для ИС, содержащей цифровое специализированное КУ:

. (3.33)

Анализируя соотношение (2.33) можно сделать вывод от том, что смещённая составляющая ошибки σ_см возрастает при увеличении параметра регуляризации α и при увеличении шага дискретизации h.

Найдём соотношение, определяющие зависимость несмещённой составляющей ошибки σ_нс от параметра регуляризации α для ИС (Рис.3.1), содержащей цифровое специализированное КУ, на вход которого поступает дискретный белый шум n(z) с нормальным законом распределения и дисперсией D.

Спектральная плотность сигнала S_ку(jλ) на выходе цифрового специализированного КУ описывается соотношением:

. (3.34)

Тогда дисперсия сигнала D_вых на выходе КУ определяется соотношением:

, (3.35)

где Т - нормирующий множитель, равный периоду дискретности.

Преобразуем (3.35) к виду:

. (3.36)

Тогда (3.36) можно записать в виде:

, (3.37)

где

. (3.38)

Отметим, что интеграл I_n в общем случае при любом n для устойчивой системы может быть представлен в виде (2.19). Тогда, выполнив необходимые подстановки в (2.19) и дальнейшие преобразования получим искомое соотношение, определяющее зависимость несмещённой составляющей ошибки σ_нс от параметра регуляризации α для ИС, содержащей цифровое специализированное КУ, которое реализует полученное разностное уравнение (3.10):

. (3.39)

Анализируя (3.37) с учётом полученного соотношения (3.39) можно сделать вывод о том, что несмещенная составляющая ошибки σ_нс уменьшается при увеличении параметра регуляризации α и при увеличении шага дискретизации h.

Следует отметить, что аналогично могут быть найдены соотношения определяющие зависимость несмещённой составляющей ошибки σ_нс от параметра регуляризации α для ИС, содержащей цифровое специализированное КУ, которое реализует полученные разностные уравнения (3.19) и (3.28).