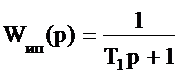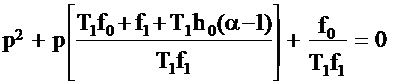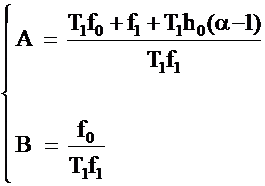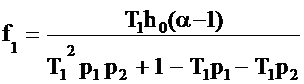СОДЕРЖАНИЕ

ВЫБОР ПАРАМЕТРОВ ЗВЕНА ДИНАМИЧЕСКОЙ КОРРЕКЦИИ, ОБЕСПЕЧИВАЮЩИЙ ПОДАВЛЕНИЕ ДЕЙСТВУЮЩИХ ПОМЕХ И КОМПЕНСАЦИЮ ИНЕРЦИОННОСТИ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ, МОДЕЛИРУЕМЫХ АПЕРИОДИЧЕСКИМ ЗВЕНОМ ПЕРВОГО ПОРЯДКА

Рассмотрим предлагаемую методику расчёта соотношений для нахождения численных значений коэффициентов звена динамической коррекции W_с(р), для случая моделирования ИП апериодическим звеном первого порядка [39], [40] с ПФ:

. (2.38)

С целью обеспечения подавления действующих помех и максимальной простоты специализированного КУ, выберем порядок ПФ звена динамической коррекции W_с(р) равным единице, т.е.:

. (2.39)

Подставим (2.38), (2.39) в (2.8) и стремясь к наиболее простому виду W_с(р), на основании [95] положим h₁=0. Тогда ПФ специализированного КУ будет описываться соотношением:

(2.40)

Запишем характеристическое уравнение ПФ (2.40) в виде:

. (2.41)

Положим в (2.41) коэффициенты при p равными соответственно:

. (2.42)

Система двух уравнений (2.42) содержит три неизвестных h₀, f₀, f₁. Доопределим систему, задавшись коэффициентом h₀=const.

Тогда численные значения коэффициентов f₀ и f₁ могут быть найдены по соотношениям:

. (2.43)

. (2.44)

Согласно теореме Виета запишем для корней p₁ и p₂ уравнения (2.41) соотношения:

. (2.45)

. (2.46)

Подставим (2.45), (2.46) в (2.43), (2.44) и получим соотношения для, расчёта численных значений коэффициентов f₀ и f₁ по заданным корням характеристического уравнения (2.41):

. (2.47)

. (2.48)

Как видно из полученных соотношений (2.47) и (2.48), численные значения коэффициентов f₀ и f₁ определяются корнями p₁ и p₂ характеристического уравнения (2.41), коэффициентом T₁ ПФ (2.38) и параметром регуляризации α. Численное значение коэффициента h₀ выбирается исходя из его максимальной простоты реализации в специализированном КУ.