СОДЕРЖАНИЕВЫБОР КОЭФФИЦИЕНТОВ РАЗНОСТНОГО УРАВНЕНИЯ ЦИФРОВОГО СПЕЦИАЛИЗИРОВАННОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА, ОБЕСПЕЧИВАЮЩЕГО ПОДАВЛЕНИЕ ДЕЙСТВУЮЩИХ ПОМЕХ И КОМПЕНСАЦИЮ ИНЕРЦИОННОСТИ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ, МОДЕЛИРУЕМЫХ АПЕРИОДИЧЕСКИМ ЗВЕНОМ ВТОРОГО ПОРЯДКАВоспользуемся методом декомпозиции [60] для получения разностного уравнения цифрового специализированного КУ, эквивалентного аналоговой передаточной функции (2.25). Для чего преобразуем (2.25) к виду: Пусть p1, p2, p3 - корни характеристического уравнения ПФ КУ (3.20). Положим корни p1 = p2 = p3 = p* и выполним разложение (3.20) на элементарные дроби на основании соотношения: Откуда найдём неизвестные коэффициенты a и b: Учитывая (3.21) и (3.22) преобразуем (3.20) необходимым образом и получим:
Определим в (3.21) необходимую весовую функцию [13] и запишем соответствующее ей z - изображение: Приведём (3.20) с учётом (3.6), (3.15), (3.24) к виду: Выполнив необходимые преобразования в (3.25) с учётом (3.23), получим ПФ КУ в дискретном виде: где Y3(z) - z - изображение входного сигнала КУ, B3(z) - z - изображение выходного сигнала КУ. Преобразуем (3.26) к виду: В соответствии с [12], осуществив замену: B1z0 -> B1[n], B1z-1 -> B1[n-1], B1z-2 -> B1[n-2] в (3.27), получим искомое разностное уравнение цифрового специализированного КУ: |
|
Все права на информацию для посетителей разрешены © 2011 - 2022 - Zadereyko.INFO
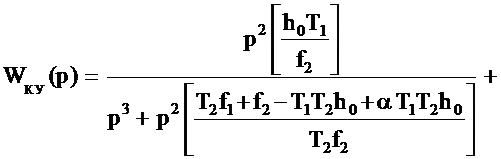




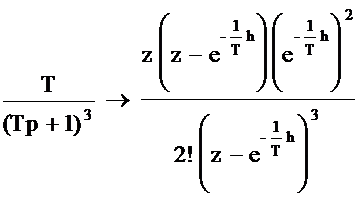
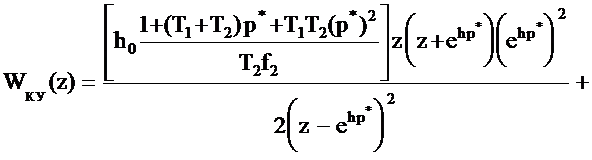 (3.25)
(3.25)