СОДЕРЖАНИЕ

МОДЕЛИРОВАНИЕ ТРАНСФОРМАТОРА

Трансформатор представляет собой магнитопровод, на котором выполнены две или более обмотки.

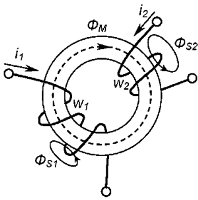
По магнитопроводу замыкается магнитный поток Ф_м, который обеспечивает магнитную связь между обмотками. Существуют потоки рассеяния Ф_э1 и Ф_э2, создаваемые токами i₁, и i₂, не замыкающиеся по магнитопроводу и не являющиеся общими для обмоток. Обмотки имеют омические сопротивления r₁ и r₂, а также другие паразитные параметры, например, межвитковые и межобмоточные емкости.

Идеальный трансформатор представляется элементом, в котором отсутствуют потоки рассеяния, активные сопротивления обмоток, паразитные емкости. Индуктивность намагничивания равна бесконечности, т.е. ток намагничивания равен 0. При этом обмотки пронизывают одинаковые потоки и по закону электромагнитной индукции для обеих обмоток можно записать, что:

u₁ = e₁ = dΨ_M/dt = w₁•dΨ_M/dt; u₂ = e₂ = dΨ_M/dt = w₂ = dΨ_M/dt;

e₂ = e₁w₂/w₁ = e₁n

Здесь n=w₂/w₁ — коэффициент трансформации трансформатора. Из закона сохранения энергии следует, что:

i₁ • e₁ = i₂ • e₂, т.е. i₂ = i₂/n

Это же вывод можно получить, используя закон полного тока с учетом того обстоятельства, что i_μ=0:

Σiw = 0; i₁ • w₁ = i₂ • w₁

При указанных допущениях трансформатор можно представить эквивалентной схемой, изображенной на Рис.1.:

Рис. 1. Эквивалентная схема трансформатора

Модель крайне проста, однако применяется крайне редко, т.к. не позволяет учесть принципиально важных для трансформатора явлений — накопления энергии в магнитопроводе и необходимость восстановления магнитного состояния сердечника.

Для ее учета представляют трансформатор совершенным элементом, в котором отсутствуют потоки рассеяния, но имеется конечная величина индуктивности намагничивания L_μ. Последняя определяет ток намагничивания, протекающий по первичной обмотке, и приводит к эквивалентной схеме представленной на Рис.2.

Рис. 2. Полная эквивалентная схема трансформатора

В ряде случаев, особенно при расчете достаточно простых цепей, представляется удобным «привести» трансформатор к одной из сторон: первичной или вторичной, представив процесс передачи энергии через магнитопровод непосредственным подключением нагрузки к цепи источника энергии.

Если, например, трансформатор нагружен на активное сопротивление R, то величина тока нагрузки в первичной цепи определится:

i₁₂ = i₂ • n = u₂n/R₂

Тогда эквивалентное сопротивление нагрузки, подключенной к первичной цепи, равно:

R'₂ = u₁/i₁₂ = u₁ • R₂/ u₂ • n = R₂/n²

Несложно показать, что индуктивность, включенная в качестве нагрузки, приводится к первичной стороне в виде:

L₂ = L₂/n²

Емкость — в соответствии с соотношением:

С'₂ = С₂ • n²

Таким образом; эквивалентная схема «приведенного» к первичной обмотке трансформатора имеет вид (Рис. 3):

Рис.3. Эквивалентная схема «приведенного» к первичной обмотке трансформатора

Выполнение трансформатора с сердечником из магнитопровода в виде ферромагнетика приводит к нелинейной зависимости L(i).

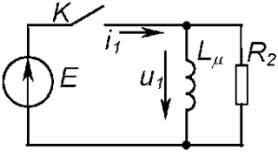
Совершенная эквивалентная схема трансформатора с учетом L_μ позволяет учесть важнейшую особенность его — необходимость восстановления исходного магнитного состояния сердечника. Так, с учетом приведенной выше эквивалентной схемы, можно показать, что подача импульсного напряжения на трансформатор в соответствии со схемой Рис. 4, приведет к тому, что на вторичной обмотке будет формироваться импульс напряжения вида (Рис. 5):

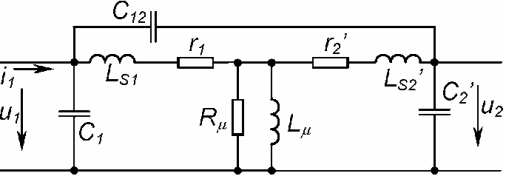
Таким образом, при расчете трансформаторных цепей необходимо учитывать время восстановления магнитного состояния и формировать специальными цепями (цепями восстановления), форму напряжения при восстановлении. В показанном выше случае, при размыкании ключа К и отсутствии нагрузки, напряжение на ключе может стремиться к бесконечности, что приведет к его пробою.

Приведенные модели трансформатора являются низкочастотными, т.к. не учитывают влияние индуктивностей рассеяния и емкостей между обмотками. Полная эквивалентная схема трансформатора, приведенная к первичной цепи имеет вид Рис. 6:

Рис.6. Полная эквивалентная схема трансформатора, приведенная к первичной цепи

Здесь L_s1, L_s2' — индуктивность рассеяния первичной обмотки и приведенная к первичной индуктивность рассеяния вторичной обмотки;

С₁, С₂' — емкость первичной и приведенная к первичной емкость вторичной обмотки;

С₁₂ — емкость между первичной и вторичной обмотками, R_μ — эквивалентное сопротивление, отображающее потери в магнитопроводе. Расчет переходных процессов в такой схеме, разумеется, весьма сложен, поэтому ее в ряде случаев упрощают. Дело в том, что индуктивность намагничивания имеет величину на 3-4 порядка большую, чем индуктивность рассеивания. Поэтому постоянные времени при расчете могут различаться на 4 и более порядков. С другой стороны, в зависимости от того, является трансформатор понижающим или повышающим, существенно меняется приведенная величина индуктивности рассеивания L_s1 (спорное утверждение!):

Ls₂ = Ls₂/n²

Аналогично, в повышающих трансформаторах наибольшее влияние имеет приведенная к первичной обмотке емкость вторичной С₂:

С'₂ = С₂ • n²

Как правило, индуктивности рассеяния не оказывают существенного влияния на процессы в цепях намагничивания, поэтому оказывается возможным объединить индуктивности рассеяния в одну. То же следует и для резисторов, отображающих омические потери в обмотках. Поэтому для повышающего трансформатора n>>1 эквивалентная схема трансформатора имеет вид Рис. 7, для понижающего — соответственно, Рис. 8: