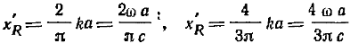СОДЕРЖАНИЕИЗЛУЧЕНИЕ ЗВУКА ПОРШНЕВЫМ ИЗЛУЧАТЕЛЕМ
Очевидно, что для этого к источнику должна быть подведена мощность. Предположим, что источник звука представляет собой невесомый поршень, колеблющийся без трения в бесконечной стене. Если вокруг поршня создан вакуум, то ясно, что для приведения поршня в колебание достаточна бесконечно малая возбуждающая сила и соответственно такая же мощность. Однако картина резко изменится, если поршень окружает обычная среда. Оказывается, что при этом к поршню должна быть приложена определенная возбуждающая сила F, состоящая из активной и реактивной составляющих: F = F1 + jF2 = (rR + jxR) (17) где Для того чтобы выяснить роли величин rR + xR, умножим обе части уравнения (17) на
PA = Полученное выражение аналогично, выражению для полной электрической мощности в цепи с индуктивностью и активным сопротивлением: P = I2R + jI2ωLc В идеальном случае неограниченной среды активная мощность Она теряется поршнем необратимо и должна непрерывно пополняться.
Формально, поскольку процесс имеет необратимый характер, можно сказать, что мощность
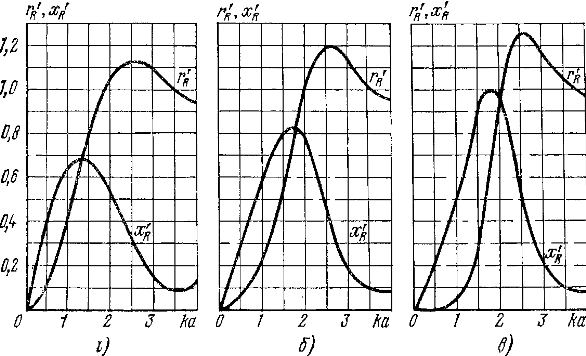
P = Обычно среда, в которой происходит распространение звука, ограничена (например, поверхностями помещения, границами земной атмосферы). Казалось бы, что после возбуждения конечного объема среды источнику больше не на что затрачивать свою мощность, но необходимо помнить, что реальные среды обладают поглощением, т. е. при распространении звука часть его энергии превращается в тепло. Потери мощности имеют место также при отражении звука от ограничивающих объемов звукопоглощающих поверхностей. Поэтому при распространении звука в конечных объемах источник должен также доставлять мощность для покрытия этих потерь. Что касается реактивной мощности Величины rR + xR не являются постоянными, а зависят от вида источника, его поверхности, от соотношения между размерами источника и длиной волны излучаемого звука, а также от удельного акустического сопротивления среды. Полное сопротивление излучения zR может быть выражено как zR = rR + jxR = ρcS(r'R + jx'R) (20) где S — поверхность источника; ρc — волновое или удельное акустическое сопротивление среды; r'R, x'R — соответственно безразмерные удельные коэффициенты активного и реактивного сопротивлений, отнесенные к единице поверхности источника и к среде с единичным удельным акустическим сопротивлением. Значения r'R и x'R могут быть вычислены с помощью довольно сложных математических выкладок. Результаты этих вычислений для поршня, колеблющегося в бесконечной стене (Рис. 9,а), изображены графически на Рис. 10,а. Здесь коэффициенты r'R и x'R выражены в зависимости от значения ка = 2π/λ= 2πfa/с=ωa/c, где а — радиус поршня. Рис. 9. Три типа поршневых излучателей: а — круглый поршень в бесконечной стене; б — односторонний поршень без экрана; в — двусторонний поршень без экрана При больших и малых значениях ka, т. е. соответственно на высоких и низких частотах, для коэффициентов r'R и x'R получаются следующие приближенные выражения: при ka>>1 при ka>>1 r'R=1; x'R = 0. Коэффициент x'R определяет реактивную часть сопротивления излучения на низких частотах (при малых ka).
Полное сопротивление этой части Оно обусловлено некоторой соколеблющейся или присоединенной массой 8/3ρa3. Поэтому величину xR иногда называют инерционной частью сопротивления излучения. При колебаниях поршня не в бесконечной стене возможны два случая: одна поверхность закрыта и не излучает (Рис. 9,б), обе поверхности поршня открыть и излучают (Рис. 9,в). Во втором случае при движении поршня, например, вправо, он создает сгущение правой стороной и разрежение — левой. Если взять какую-либо точку среды, находящуюся в плоскости поршня, то очевидно, что сгущения и разрежения доходят до нее одновременно и нейтрализуются. Следовательно в плоскости поршня звуковое давление равно нулю. Возьмем теперь точку О, лежащую где-либо вне плоскости поршня. Пути колебаний (сгущения и разрежения) до точки О от обеих сторон поршня различаются на какую-то величину ∆l. Соответственно разность фаз φ колебаний, приходящих от обеих сторон поршня, равна уже не π, а φ = π + 2π∆l/λ. Член 2π∆l/λ должен быть достаточно большим, чтобы в точке О сгущения и разрежения не нейтрализовались. На низких частотах при заданной разности путей ∆l значение 2π∆l/λ мало. Поэтому будет мало и развиваемое звуковое давление. Чтобы увеличить звуковое давление на низких частотах, необходимо поршень помещать в бесконечную стену (при этом ∆l=∞), а практически — в экран достаточно больших размеров. Обычно вместо экрана применяют оформления в виде открытых с задней стороны ящиков, о чем подробнее будет сказано далее.
В поршне с закрытой задней поверхностью, изображенном на Рис. 9,6, нейтрализация звукового давления, создаваемого передней поверхностью поршня, отсутствует. Однако на низких частотах звуковое давление, создаваемое таким поршнем, меньше, чем звуковое давление, создаваемое поршнем, колеблющимся в бесконечной стене. Это происходит за счет того, что в первом случае энергия излучается в окружающую среду в пределах телесного угла 4π, в то время как во втором она излучается только в пределах угла 4π. На высоких частотах разница будет небольшой из-за направленности излучения, о чем будет сказано далее. Следовательно, для излучения звуков низких частот важно помещать поршень в большой экран. На Рис. 10 кроме кривых r'R и x'R для поршня в бесконечном экране (а) приведены кривые r'R и x'R для поршня, закрытого с одной стороны (б), и кривые r'R и x'R для поршня, открытого с двух сторон (в) для малых значений ka аналогично (21) значения соответственно равны: r'R Рис. 10. Удельное сопротивление излучения различных видов излучателей Соответственно значения x'R будут: Отсюда можно получить для величины соколеблющейся массы: mR = 2ρa3, mR = (4/3)ρa3 (23) Сопротивление излучения, будучи весьма малым для поршня, малого по сравнению с длиной волны и колеблющегося в бесконечном экране, становится еще меньше, если этот поршень колеблется без экрана или излучает только одной стороной. Таким образом, для излучения значительных мощностей поршень, малый по сравнению с длиной волны и имеющий малое сопротивление излучения, должен иметь весьма большие колебательные скорости [см. (19)]. Рассмотрим излучение поршня, находящегося в бесконечном экране (Рис. 11). Положим, что мы находимся в точке, расположенной на прямой, идущей под углом а к оси поршня. Если эта точка расположена достаточно далеко от поршня, то можно считать, что все прямые, проведенные от различных точек поверхности поршня к ней, будут идти почти параллельно. Колебания же, распространяющиеся вдоль этих прямых, придут в эту точку с разными фазами, Отсюда колебания от крайних точек поршня диаметром d придут в рассматриваемую точку со сдвигом фазы φ = (2πd/λ) • sinα = (2πdfd/c) • sinα При достаточно большом отношении d/λ колебания от разных точек диафрагмы будут приходить в фазе или с небольшой разностью фаз только в направлении оси или близком к ней (а мало). Рис. 11. Излучение поршня в разных направлениях относительно его оси |
Количественно направленность излучения определяется характеристиками направленности, обычно изображаемыми в полярных координатах. Характеристика направленности представляет собой графическое изображение относительной величины звукового давления Rα, развиваемого излучателем в данном направлении, по сравнению с давлением, развиваемым излучателем в направлении оси, в зависимости от угла, образованного осью излучателя и направлением излучения. Так, например, измерив на Рис. 12 радиус-вектор, получим, что звуковое давление на любом расстоянии от излучателя под углом 15° к его оси составляет 0,8 значения звукового давления на том же расстоянии по оси излучателя. При излучении поршня без экрана характеристика направленности изображается косинусоидой (восьмеркой при построении в полярных координатах).
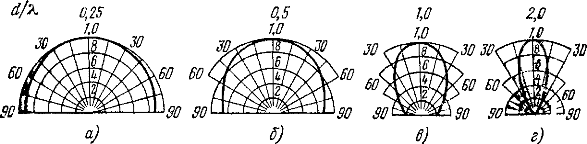
На Рис. 13 при различных отношениях d/λ изображены характеристики направленности излучения поршня, помещенного в бесконечный экран для различных значений отношения диаметра поршня к длине волны. Направленность излучателя может быть оценена и через так называемый коэффициент концентрации — отношение мощности, излученной направленным излучателем, развивающим звуковое давление, такое же, как и у ненаправленного излучателя на его оси к мощности, излученной последним. Коэффициент концентрации для ненаправленного излучателя равен единице, а для излучателя с восьмерочной (косинусоидальной) характеристикой направленности — трем. Направленность реальных излучателей в зависимости от частоты описывается более сложным образом и практически определяется при измерениях.
Рис. 13. Характеристики направленности излучения поршня в бесконечном экране
|
|
Все права на информацию для посетителей разрешены © 2011 - 2024 - Zadereyko.INFO


 (22)
(22)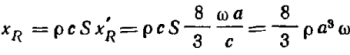
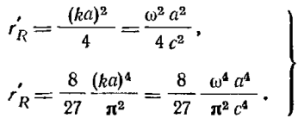 (23)
(23)