СОДЕРЖАНИЕ

КОЛЕБАНИЯ И ВОЛНЫ В СРЕДЕ

Рассмотрим процесс возникновения и распространения колебаний в воздушной среде.

Пусть имеется бесконечно большая жесткая стенка С, в которой может передвигаться вправо и влево относительно своего положения равновесия поршень П (Рис. 4). Пусть, например, в данный момент поршень идет вправо, толкая находящиеся перед ним частицы воздуха.

Частицы, отклоняясь от своего положения равновесия, в свою очередь толкают частицы, находящиеся вправо от них, т.е. следующие за ними и т.д.

Справа от поршня образуется сгущение воздуха или область с повышенным атмосферным давлением.

Толчки от одной частицы воздуха к другой передаются все дальше от поршня, вследствие чего вправо от него распространяется сгущение.

Пусть теперь поршень после того, как он достиг своего крайнего правого положения, начал передвигаться влево. Тогда перед ним образовывается разрежение воздуха, или область с пониженным атмосферным давлением. Поскольку у поверхности поршня создалась область разрежения, туда устремятся примыкающие к ней частицы воздуха. На том месте, где они находились, в свою очередь образуется область разрежения, в которую устремятся другие, примыкающие к этой области, частицы воздуха. В результате вправо от поршня будет распространяться разрежение. Таким образом, колебания поршня периодически вызывают во внешней среде (воздухе) возмущения в виде сгущения и разрежения, причем одному периоду колебаний (движение поршня вперед и назад) соответствует одно сгущение и одно разрежение.

Давление р, измеренное в какой-то определенной точке среды, окружающей поршень, изменяется в зависимости от времени по закону, подобному закону движения поршня. При колебательном движении поршня давление в рассматриваемой точке сначала нарастает, становясь больше атмосферного давления р₀, а затем спадает до значения меньшего, чем атмосферное давление, и, наконец, опять увеличивается до значения р₀.

Графически процесс изменения давления во времени в данной точке среды изображен на Рис. 5, который соответствует движению поршня, совершаемому по синусоидальному закону. Значение давления в каждый момент времени называется его мгновенным значением. Давление в каждой данной точке можно представить в виде суммы двух составляющих: постоянной, равной атмосферному давлению, и накладывающейся на него переменной. Последняя обычно называется звуковым давлением. Период изменения давления Т равен периоду колебаний поршня.

Амплитуда же звукового давления пропорциональна амплитуде колебаний поршня. Заметим, что на Рис. 5 амплитуда звукового давления сильно преувеличена по сравнению со значением атмосферного давления из-за невозможности изобразить величины давлений в истинном соотношении, так как амплитуда звукового давления даже самых громких звуков составляет меньше одной тысячной доли от величины атмосферного давления.

Рис. 4. Образование звуковых волн в среде

Рис. 5. Зависимость давления в среде от времени

Звуковое давление, как и всякое давление, измеряется силой, действующей на единицу площади. Поэтому в акустике за единицу звукового давления принято такое давление, при котором на площадь в 1 м² действует сила, равная 1 Н. Эта единица звукового давления называется паскаль (Па). Паскаль является удобной единицей измерения, так как в большинстве случаев значения звукового давления изменяются от сотых долей паскаля до нескольких его единиц. Звуковое давление при средней громкости разговора составляет доли паскаля. Среднее атмосферное давление, соответствующее давлению ртутного столба высотой 760 мм, составляет приблизительно 10 Па.

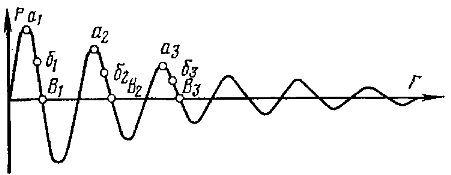
Как и другие акустические величины, звуковое давление также измеряется в действующих значениях.

Состояние среды в рассматриваемой точке можно охарактеризовать не только изменением давления в ней, но и скоростью частиц воздуха или смещением их относительно положения равновесия. При синусоидальных колебаниях поршня кривые скорости или смещения частиц в зависимости от времени имеют также синусоидальную форму.

На Рис. 6 изображено изменение во времени скорости частиц, обычно называемой в акустике колебательной скоростью. Колебательная скорость х в разные моменты времени имеет разные значения и знаки. Таким образом, в звуковом поле каждая частица среды находится в определенной фазе колебаний.

Итак, колебания источника звука (например, поршня) вызывают в среде сгущения и разрежения. Область, в которой наблюдаются сгущения и разрежения, называется звуковым полем. Сгущения и разрежения распространяются в среде с определенной скоростью, называемой скоростью распространения звука.

Ее значение зависит от характера и состояния среды. Так, скорость звука в газовой среде:

,

где р₀ — постоянное (атмосферное) давление; γ — показатель адиабаты, те отношение теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме. Это отношение для воздуха равно 1,4; ρ — плотность воздуха, равная при 0°С и 760 мм рт. ст. 1,3 кг/м³.

Рис. 6. Зависимость колебательной скорости в среде от времени

Рис. 7. Зависимость звукового давления от расстояния до источника

Для воздуха при этих условиях скорость распространения звука равна 331 м/с, а при 20⁰С она повышается до 344 м/с.

Скорость звука никоим образом не следует смешивать с колебательной скоростью частиц среды. Колебательная скорость частиц среды в зависимости от различных условий (например, от амплитуды, частоты колебаний источника звука) может иметь разные значения, при этом во много раз меньшие скорости распространения звука. Процессы колебаний частиц среды и распространения звука различны и по существу. В то время как звук при отсутствии препятствий может распространяться в среде сколь угодно далеко от источника, частицы среды колеблются около своего положения равновесия и поступательного движения не имеют.

Если одновременно измерить звуковое давление в различных точках прямой в направлении распространения звука, то с помощью полученных значений можно построить кривую зависимости звукового давления ρ от расстояния r. При синусоидальных колебаниях источника звука эта кривая имеет показанную на Рис. 7 форму, также близкую к синусоиде. Правда, полученная кривая будет отличаться от идеальной синусоиды: последующие амплитуды ее уменьшаются по мере удаления от источника в результате того, что энергия звука распределяется на все большую поверхность и поглощается в самой среде.

Каждой точке, расположенной на кривой, соответствует своя фаза колебания. Однако можно указать некоторое число точек с равными фазами. Так, например, в точках α₁, α₂, α₃ имеет место максимум звукового давления. Одной и той же фазой характеризуются также колебания в точках σ₁, σ₂, σ₃. Какое же расстояние разделяет точки с одинаковой фазой? Известно, что за один период источник звука посылает в среду одно сгущение и одно разрежение. Рассматривая Рис. 7, видим, что отрезок α₁, α₂ или σ₁, σ₂, равен отрезку β₁, β₂, т. е. отрезку, в котором укладывается одно разрежение и одно сгущение. Так как сгущения и разрежения перемещаются со скоростью звука, то за время Т, равное одному периоду, звуковые колебания распространяются на расстояние

λ = cT или λ = с/f (12)

Расстояние λ между самыми близкими точками (например, β₁, β₂), в которых колебания находятся в одной и той же фазе, называется длиной волны. Так, для частот звука от 50 до 10 000 Гц длины волны в воздухе изменяются oт 6,8 м до 3,4 см.

Разность фаз между точками, разделенными расстоянием nλ, равна 2πn, где n — целое число. Разность фаз φ между точками, находящимися на расстоянии l, может быть найдена из соотношения φ/2πn = l/λ

Отсюда

φ = 2πl/λ = kl (13)

где

k =2π/λ = 2πf/с = ω/с

Величина k в акустике обычно называется волновым числом. Через все точки, в которых колебания находятся в одной фазе, можно провести поверхность. Эта поверхность называется волновой или фронтом волны. В зависимости от формы, которую имеет поверхность фронта волны, различают волны сферические, плоские и т.д. Представим себе источник звука в виде пульсирующего шара, например резиновой оболочки, в которую попеременно нагнетается и из которой откачивается воздух. Такой источник звука посылает в среду сгущения и разрежения равномерно во все стороны, возбуждая сферические волны. Но на большом расстоянии от источника отдельные участки поверхности фронта сферической волны можно считать плоскими.

Практические источники звука обычно не дают ни той ни другой формы волны в чистом виде. При возбуждении звуковых волн энергия от источника поступает в среду. Благодаря этой энергии возникают колебательные движения частиц среды. Энергия этих колебаний может передаваться телам, помещенным в звуковое поле. Энергию звукового поля можно характеризовать количеством энергии, проходящей через единицу площади, расположенной в поле перпендикулярно направлению распространения звука за единицу времени (Рис. 8). Эта величина называется интенсивностью звука и измеряется в ваттах на квадратный метр.

Для сферической волны по заданной интенсивности на заданном расстоянии от источника легко определить мощность источника. Действительно, на расстоянии r от источника соответствующая сферическая поверхность равна 4πr². Если через каждый квадратный метр этой поверхности проходит мощность P, то мощность, проходящая через всю поверхность, составит 4πr²l. Эту мощность Р должен доставить источник.

Следовательно,

P = 4πr²l или I = P/(4πr²) (14)

Интенсивность в сферической волне обратно пропорциональна квадрату расстояния от источника. Но интенсивность связана со звуковым давлением в сферической волне соотношением I—р²/(ρс), здесь ρс — волновое или удельное акустическое сопротивление среде, представляющее собой произведение плотности среды ρ на скорость звука с в ней. Для воздуха при 20° С и 760 мм рт. ст. ρс = 415 кг/(с-м²).

Учитывая это, получаем:

р²/(рc) = P/(4πr²)

или

т. е. звуковое давление в сферической волне обратно пропорционально расстоянию от источника звука. Звуковые давления р₁ и р₂ в точках, расположенных от источника на расстояниях r₁ и r₂ связаны соотношением

р₁ / р_{2 =} r₁ / r₂

Для плоской волны ни звуковое давление, ни интенсивность в какой-либо точке не зависят от положения точки в пространстве. Для плоской волны существуют следующие простые соотношения между звуковым давлением р, колебательной скоростью и интенсивностью I:

Pис. 8. Поток звуковой энергии через поверхность

= р/(рc) (16)

где р и могут быть выражены либо в амплитудных, либо в действующих значениях. Связь между I и р такая же, как в сферической волне.

Эти соотношения аналогичны закону Ома и зависимости мощности от тока в напряжения в электрической цепи с активным сопротивлением.

На практике при звуковом давлении l Па колебательная скорость согласно (16) будет = 1/415 = 2,4•10^-8 м/c. Колебательное смещение на частотах 100, 1000 и 10000 Гц согласно (2) соответственно равно: x₁₀₀ = 2,4•10^-3/(2•π•100) = 3,8•10^-6 м, x₁₀₀₀ = 3,8•10^-7 м, x_{10 000} = 3,8•10^-8 м. Амплитудные значения смещений будут в √2 больше. Ускорения на этих частотах согласно (2) ₁₀₀ = 2•π•100•2,4•10^-3 = 1,5 м/с², ₁₀₀ = 15 м/с², = 150 м/с², т. е. будут довольно большими.

Так как значения акустических величин меняются в очень широких пределах, то их удобно выражать не в абсолютных значениях, а в логарифмических. К тому же громкость звука приближенно пропорциональна логарифму акустических величин (звукового давления, интенсивности и т.п.). Для вычисления таких логарифмических значений (уровней) пользуются следующими зависимостями.

Для звукового давления

N = 20lg(р/р₀₀)

Для интенсивности

M = 10lg(I/I₀₀)

Величины N и М измеряются в децибелах (дБ). В качестве р₀₀ и I₀₀ обычно принимаются значения соответственно 2•10^-5 Па и 10^-12 Вт/м², уровень которых называется стандартным нулевым.

Предположим, что следует определить уровень звукового давления 2 Па:

N = 20lg(2/2•10^-5) = 20lg10⁵ = 20•5 = 100 Дб

Уровень звукового давления в 1 Па будет равен 94 дБ.