СОДЕРЖАНИЕМЕТОД КОНТУРНЫХ ТОКОВВведем понятие вектора-столбца контурных токов I. Размер вектора [σ,1], он имеет вид: Элементы матрицы Γ показывают, как k-тый контур входит в s-тую ветвь схемы. Очевидно, матрицу Γ можно использовать для связи величин контурных токов с токами ветвей. Для этого необходимо выполнить умножение матрицы Г на вектор l. Для этого, очевидно, необходимо транспонировать матрицу Г заменив индексы у элементов местами: [Гij]t = [Гji]. Теперь матрица Гt имеет размер [l, σ], тогда можно осуществлять умножение: Гt • I = Iв Последнее уравнение отображает зависимость Ι токов ветвей от σ контурных токов. Выберем последние в качестве независимых переменных, т.е. будем искать контурные токи, протекающие, по определению, через хорды схемы. Рассмотрим уравнение по закону Ома в виде: Uв = Zв • Iв + Eв Подставим в это уравнение значение Iв, равное Гt·I. Получим: Uв = Zв • Гt • I + Eв Умножим последнее равенство на матрицу контуров Г слева. Получим: Гt • Uв = Г • Zв • Гt • I + Г • Eв По второму закону Кирхгофа Г · Uв = 0, тогда введем соответствующие упрощения: Г • Zв • Гt = Z Г • Eв = - E => Z • I = E Рассмотрим размерность полученных выражений: [Гt] = [l, σ], Zв = [l, l] [Гt• Zв] = [l, σ], Г = [σ, l] => Z = [σ, σ] Таким образом, матрица Z - квадратная матрица размера [σ, σ], которая получила название матрицы сопротивлений схемы: Вектор E имеет размерность: Г = [σ, l], Eв = [l, 1] => E = [σ, 1] Вектор E - вектор э.д.с. схемы. Нахождение Z и E не представляет проблем, т.к. все компоненты этих матриц известны. Таким образом, мы приходим к матричному уравнению вида соответствующему σ скалярных уравнений, решение которых можно осуществить, обратив матрицу Z: I = Z-1 • E Z • I = E, Таким образом, число скалярных уравнений или порядок векторного уравнения снижен с 2Ι до σ. Принципиальных трудностей при решении уравнения нет. На практике, особенно при решении уравнений для реальных электрических схем, получил большее распространение метод узловых потенциалов в матричном виде, который в ряде случаев более удобен.
|
|
Все права на информацию для посетителей разрешены © 2011 - 2024 - Zadereyko.INFO
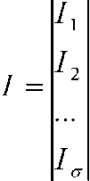
![Описание Z - квадратной матрицы сопротивлений размера [σ, σ] Описание Z - квадратной матрицы сопротивлений размера [σ, σ]](konspektu_lekciy_risynki/shemotehnika/konspect_shemotehnika139.png)